マネジメント8　決断における意思のばらつき

決断における意思のばらつき
決断における意思のばらつきということで、製品品質と同様に業務品質を上げるための方法になります。
業務改善につなげ収益につなげるようにしていきましょう。

ばらつきとは

ばらつきの考え方はバイアスと同様に品質を考える上では重要です。
業務の効率化・業務品質、ビジネスにおける戦略、製品のイメージなどたくさんの事柄に関わってきます。

製品の製造においてばらつきは大変重要な項目になります。
製品の製造におけるばらつきの考え方はこちらのページに詳しく載せています。
「ばらつきと工程能力」

決断におけるばらつきとは

ばらつきとは「ノイズ、測定間の差異」のことです。
特にこの「決断における意思」の場合は考え方の差異になります。
実際に考えによる一貫性に近いものがあります。

そのため、時間や個人ごとによりこの考え方のばらつきが出てきます。

会社の中でこんな感じになっていませんか？

考え方のばらつきが大きく現れている状態と言えます。
ノイズが大きいとも言えます。

考え方の差異、それは時間や個人ごとに出てくる

ばらつきは管理するべき？

実際にそのバイアスを管理すべきなのでしょうか？

ここの考え方は決断における意思のバイアスと全く同じです。

工場などの生産現場で物事を考えてみましょう。
「ばらつきと工程能力」でも詳しく話をしていますが、製品にはばらつき・偏りがありそれを考慮した品質確保が重要です。
そのため製品には規格があり、それは製品を世の中に出せる合格範囲となって品質が保たれます。

自然現象としてのばらつき方は正規分布で表されます。
製品製造の偏り、ばらつきというのは以下の図のような状態です。

青で表した曲線は理想的な目指す分布で、赤で表した曲線はばらつきが大きい分布、茶色で表した曲線は偏りがある分布になります。

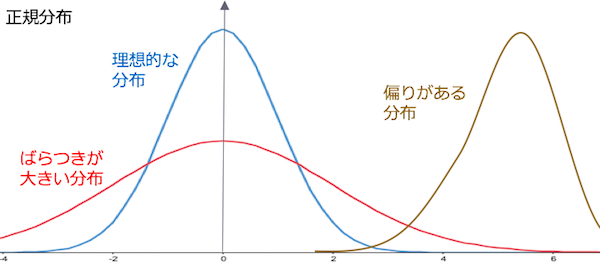
理想的な目指す分布に近づくように調整していきます。
これにより手直しや廃棄が少なくなり収益の改善を図っています。

全く同じことが、他の業務においても言えます。
製造業・工場がこれだけ品質確保、効率化と言っているのに業務自体にはあまり言われません。

目的のものがまとの中心と考えると、他の業務のおける理想的な分布、ばらつきが大きい分布、偏りがある分布は以下のようになります。

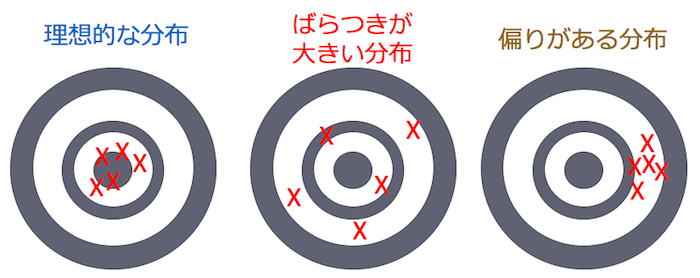
業務によっては実際に目に見える部分が少ないのと、品質の良い悪いの判断が難しいということが挙げられます。
ですが管理することで非常に会社にとって有益になります。

ばらつきはノイズ・差異がある分布の状態のため以下のように修正が必要になります。

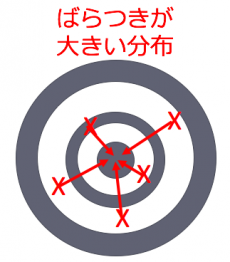
業務の効率化・業務品質保障のためには管理が必要

以下の本も業務改善に対しての考え方が詳しく載っています。
参考にしてみてください。
6ステップで職場が変わる！ 業務改善ハンドブック

考え方のばらつきの種類

先ほどから述べているように、ばらつきは「ノイズ・差異」です。
考え方での「ノイズ・差異」にはいくつか種類があります。

時間によるばらつき

時間に関係する考え方のばらつきになります。
同じ案件に対する決定内容も時間が違うと決定内容が異なってきてしまう場合です。

この限りではありませんが、一例として載せました。

・担当者の気分の変化
判断や決定は人間です。
人間なので気分の変化により決定内容にも変化してしまいがちです。

・楽しい時　→　比較的案件を容易に判断
・怒っている時　→　比較的案件を厳しく判断

などのように変えてしまう場合があります。

・直前の判断材料の属性の変化
判断する材料が時間経過に伴い変化するもの（変化量と材料自体の変化）に対して担当者の中で判断が曖昧なままだと差異が発生します。

・意志力の変化
バイアスの際にも述べましたが、しっかり物事を判断する力「意志力」は体力と同じように1日のうちに消耗していきます。

その意志力は消耗するため、目覚めた後（通常勤務なら午前中）なら難しい判断でも比較的正確になります。
逆に消耗した後（通常勤務なら午後以降）の場合は判断に対してミスを起こしやすくなっています。

時間により判断内容が変化してしまって起こる「ばらつき」

個人ごとのばらつき

個人の間で関係する考え方のばらつきになります。
同じ案件に対しても人が異なると決定内容が異なってきてしまう場合です。

こちらも、この限りではありませんが、一例として載せました。

・担当者の性格
担当者の性格でも案件に対するばらつきが発生します。

他者と比較して
・判断内容が甘め　→　比較的案件を容易に判断
・判断内容が慎重　→　比較的案件を厳しく判断

・判断材料の違い
判断材料が個人毎に異なることにより判断が異なり意思のばらつきが起こります。

・判断材料の違い
・グループ分け、セグメントの違い
・各要素の違い

違いにより精度、ばらつきが生まれてきます。
これは理想的な分布に近づけるためにも判断材料が

・判断方法の違い
判断方法が個人毎に異なることにより判断が異なり意思のばらつきが起こります。
・優先順位の違い
・評価の判断方法
・作業手順

個人毎に判断内容が変化してしまって起こる「ばらつき」

意思のばらつきの事例

ビジネス内で直接ばらつきに関連する事例はありません。
バイアスと異なり、トップの判断だけでなく細かい部分の積み重ねにより発生する場合が多いからです。

1つは演習としての意思のばらつきが発生する例を紹介します。
もう1つは意思のばらつきが関連するとは言えませんが、考え方・見方を修正することにより改善できたビジネス内での事例を紹介します。

意思のばらつきの例

例として以下の状況の場合の選択になります。

今、あなたは就職先を探しています。
両方あなたが就きたい業種・職種の企業になります。
従業員の数・規模は同じです。

以下の企業のどちらに就職したいですか？

企業①
平均年収：８００万円

企業②
平均年収：６００万円

企業③
平均年収：５５０万円

次に上で示した企業の中身を見てみます。
各企業、全従業員数を10人とした場合です。

企業①　平均年収８００万円の年収分布
２００万円：7人
２００万円：2人
６０００万円：1人

企業②　平均年収６００万円の年収分布
２００万円：2人
３００万円：1人
７００万円：3人
８００万円：4人

企業③　平均年収５５０万円の年収分布
５５０万円：10人

・中央値：順位が真ん中の人の年収
・最頻値：最も多く当てはまる人の年収
・標準偏差σ:ノイズの度合い
(平均値±σ→全体の６８.３%の分布の範囲値)

もう一度訊ねます。

今、あなたは就職先を探しています。
両方あなたが就きたい業種・職種の企業になります。
従業員の数・規模は同じです。

以下の企業のどちらに就職したいですか？

企業①
平均年収：８００万円
中央値：２００万円
最頻値：２００万円
標準偏差：１７３４万円

企業②
平均年収：６００万円
中央値：７００万円
最頻値：８００万円
標準偏差：２４５万円

企業③
平均年収：５５０万円
中央値：５５０万円
最頻値：５５０万円
標準偏差：０万円

あなたの意思に変化はありましたか？
新たな情報にあなたの判断材料が他に含まれていましたか？
もし、変化があったならそれも「ばらつき」（ノイズ、差異）です。

理想的な分布に近づけるには判断材料も重要です。
集団全体の傾向とグループに分けた場合の傾向が異なることがあります。
それらを考慮に入れた判断材料も必要になります。

変化があったならそれも「ばらつき」

ビジネス内での例〜日本航空の再生〜

日本航空（JAL）の事例になります。
会社更生法の適用時の日本航空の利益：2010年3月　▲1337億円（赤字）

当時の経営方法としては、ざっくり以下のようになります。

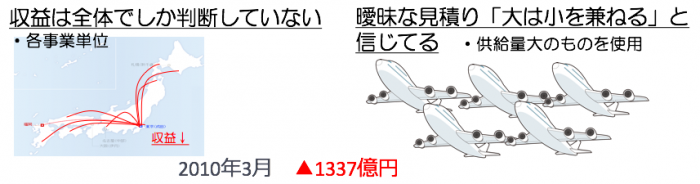
・各事業単位で収益は全体でしか判断していない
・曖昧な見積り「大は小を兼ねる」と考えていた
→経営判断のばらつきが大きかった

稲盛和夫が日本航空再生に乗り出し、以下のように改善していきました。

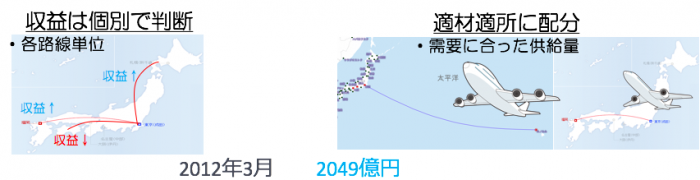
・収益は個別で判断
・適材適所に配分
→経営判断に対して適切な判断材料を使用し、個別の基準を持たせることにした。

会社更生法の適用から2年後の利益：2012年3月　　2049億円（黒字）
経営判断が理想的な分布に近づいたため、利益として結果が導けた例と言えます。

判断材料、情報を明確化、個別の基準により理想的な分布に近づけた

ばらつきを回避するには

どのようにして、ばらつきを回避していけば良いでしょうか？
まず、基本的なばらつき回避の考え方とばらつき回避のための判断アルゴリズムを説明していきます。

基本的なばらつき回避の考え方

基本的な考えを持つことでばらつきがある程度軽減され、判断が理想的な分布に近づきます。

・共通の情報
違った情報を持つとばらつきが大きくなります。
もし個人で取得した情報は共有化して共通の情報としていきます。

逆に共通の情報を常に受け取れる体制にしましょう。

・共通の判断材料
先ほどの例にもあげましたが、ばらつきの少ない理想的な分布に近づけるにはそれに適した判断材料が必要になります。
そのため、案件の品質に対する判断材料の関係性を考えなければいけません。
もちろんプラス方向の関連もあればマイナス方向の関連する項目もあると思いますが、両方入れます。

また、判断材料は変えずに共通認識として使用していきます。
変えてしまうと共通の情報、共通の判断方法があったとしても異なってきます。

・共通の判断方法
共通の判断方法を決めることにより判断の違いでの差異が現れにくくなります。

・手順を明確にする
・優先順位を明確にする
・評価の方法の判断基準を明確にする
などの方法を共通で行うようにしましょう。

ばらつきを軽減するには共通の情報、共通の判断材料、判断方法が必要

ばらつき回避のための判断アルゴリズム

ばらつきを回避するために共通の判断材料、判断方法が必要です。
ですが、判断が難しいことも多々あります。
その際に役に立つ方法になります。

この方法は判断材料に対する出現の「レア度」を数値で出すことでロジカルに判断することができます。
また、この方法は判断材料の単位があっていなくても比較できます。

・結果に関係する項目を６個以上挙げる
共通の判断材料に当てはまる項目を6個以上挙げます。
もちろんマイナス方向に関連する内容も入れます。
（その場合、標準スコアを出す際の係数は-1）

案件に対して判断項目が変化した場合、ここから始めます。
それまで一度決めたら変える必要はありません。

複数の案件を評価、比較の例：ランチの選択（判断項目）
例として、ランチのメニューの選択の例を考えます。

この場合、５種類の案件（Aランチ、Bランチ、Cランチ、ラーメン、カレー）を比較します。
判断項目として以下をあげました。
・並ぶ人の少なさ[並ぶ人数]
・見た目の単価[1-5段階]
・見た目のおいしさ[1-5段階]
・カロリー低さ[カロリー数値]
・イベントの有無[1:有、0:無]
・価格の安さ[円]

それぞれ単位は異なります。

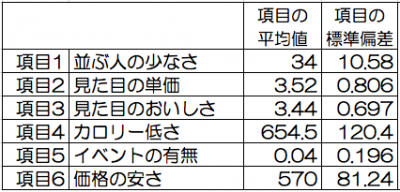
次に過去のデータより項目ごとの平均値・標準偏差を出します。

・一定量の過去のデータから項目ごとの平均値・標準偏差を出す
ある一定期間の案件に対する先ほど挙げた項目の平均値及び標準偏差値を求めます。
そのため、判断材料が過去に1つも無いものはできません。
（過去に判断材料の値が1つも無いということは、判断材料も案件に関連するとは言えないと思いますが、）

これは一度平均値・標準偏差を取得しておけば頻繁に更新する必要性はありません。
Excelで標準偏差を使用する際は「STDEV.P」関数を使います。

複数の案件を評価、比較の例：ランチの選択（過去のデータからの平均値・標準偏差）
各項目の過去１週間の案件（メニュー）の値から出しました。
項目ごとの平均値・標準偏差は次のようになりました。

次に評価をしたい値を見ます。

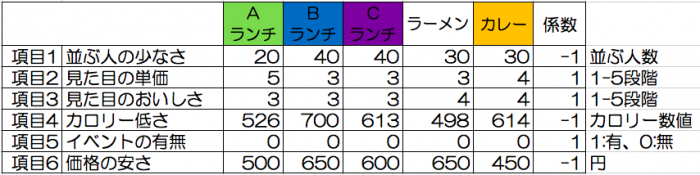
・評価したい値（案件の値）を出す
案件に対して、項目の値を埋めます。
ランチ選択は複数の案件のため、１つ案件を評価したい場合は例の一列分を埋めれば良いです。

複数の案件を評価、比較の例：ランチの選択（案件の値）
本日のランチメニューの評価値を出します。
ここではわかりやすいように係数も添えています。

係数「-1」は項目の値がマイナス方向の方が良い場合です。
また、重要度に応じてこの係数の値を大きくしても構いません。
（ただし、係数の変更は案件に対して判断項目が変化した場合にしてください。）

今回は以下のようになります。

ここから標準スコアを出していきます。

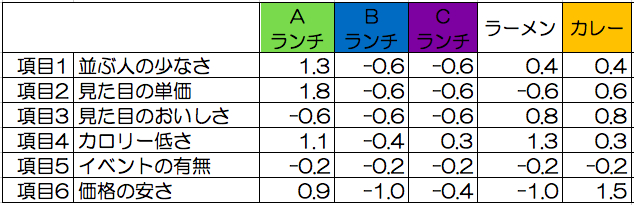
・案件毎に項目ごとの「標準スコア」を出す
「１つ案件を評価したい場合」も「複数の案件を評価、比較したい場合」も項目を埋めた後、項目に対して（案件の値x−平均値μ）/標準偏差σを出します。

ただし、判断がマイナス方向の項目に対してはこの計算結果に「-1」を掛けます。
また、項目の重要性によりこの計算結果に係数を掛けます。（基本的には係数を掛けなくて良いです。）

複数の案件を評価、比較の例：ランチの選択（標準スコア）
項目ごとに標準スコア「係数×(案件の値x−平均値μ)/標準偏差σ」を求めていきます。

・案件毎に「要約スコア」を出す
案件に対する標準スコアの平均値を求めます。（標準スコア1+標準スコア2+⋯+標準スコアn）/項目数n

複数の案件を評価、比較の例：ランチの選択（要約スコア）
先ほど求めた標準スコアから案件ごと（メニューごと）に平均値を求めていきます。

・要約スコアの順位、数値に応じて対応を決めておく
決定内容を要約スコアの値で判断していきます。

・１つ案件を評価したい場合
要約スコアの数値に対して判断内容を決定する。

・複数の案件を評価、比較したい場合
要約スコアの数値に対して判断内容を決定する。
または、要約スコアの数値の順位に対して判断内容を決定する。

複数の案件を評価、比較の例：ランチの選択（判断）
評価対応を決めておきます。
ここでは
・要約スコアが最も高いのをランチとして選択

そのため、判断は「Aランチ」になります。
これでランチを選択するのにばらつきが減りました…⁈

これらにより、共通の判断材料、判断方法が成り立ちます。
ばらつきも最小限に抑えられます。

これらの考え方は製品製造の際の「工程能力」と全く同じです。
案件に対する判断材料1つ1つに工程能力を割り当てたのと同じになります。

詳しくはこちらのページを見てください。「ばらつきと工程能力」

判断アルゴリズムを使うことで共通の判断材料と判断方法で判断できる